Задача Е. Гренки
Задачу добавил: alef
Успешно сдано решений: 13
Гренки - очень простое в приготовлении блюдо. Достаточно размешать в половине стакана теплого молока (годится и порошковое) сырое яйцо, добавить чуть-чуть (на кончике ножа) соли, дать пропитаться этой смесью кусочкам булки или батона (вообще можно использовать практически любой хлеб) толщиной около сантиметра, и обжарить их до румяной корочки на растительном масле. Кеше Канарейкину понравилось готовить гренки, и он делает это регулярно.Причем готовит он их не только из булок и батонов, но и из других видов хлеба. Однажды он оказался в гостях у своего товарища, который предложил ему приготовить гренку из одного большого хлебного изделия идеальной квадратной формы. Когда эту "супергренку" обжарили с одной стороны и перевернули на другую, Кеше пришла в голову идея слегка посыпать ее шпинатом. Однако товарищ начал возражать против таких кулинарных экспериментов. Тогда Кеша насыпал шпинат на гренку так, что засыпанной оказалась прямоугольная область.
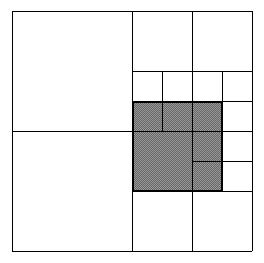
Когда гренка оказалась готова, товарищи разрезали ее на четыре одинаковых квадрата. Квадраты, которые либо были полностью засыпаны шпинатом, либо были полностью от него свободны, отложили в сторону, а каждый из оставшихся "смешанных" квадратов снова разрезали на четыре квадрата и т.д. В результате исходный квадрат оказался разрезан на квадраты, либо полностью засыпанные шпинатом, либо полностью свободные от него, как это для примера показано на рисунке. Подсчитайте, сколько получилось квадратов со шпинатом и сколько без него.
Для определенности будем считать, что размер гренки задается как 2^N х 2^N единиц, каждый единичный квадрат либо засыпан шпинатом, либо нет (таким образом, засыпанный прямоугольник можно считать образованным такими единичными квадратами).
Для удобства задания исходных данных введем систему координат: левый нижний угол исходного квадрата поместим в точку (0;0), а правый верхний – в точку (2^N;2^N). Соответствующие вершины закрашиваемого прямоугольника поместим в точки (x1;y1) и (x2;y2).
Формат входного файла input.txt
Первая строка -целые числа N, x1, y1, x2, y2 (1<=N<=30; 1<=x1<x2<=2^N, 1<=y1<y2<=2^N) через пробел.
Формат выходного файла output.txt
Первая строка - два значения через пробел - число квадратов без шпината и число квадратов со шпинатом.
Пример входного файла
3 4 2 7 5
Пример выходного файла
13 6