A. Самокат
Задачу добавил: alef
Успешно сдано решений: 1040
Студент Кеша устроился на летнюю стажировку. Кеша охотно бы ходил на работу пешком, но, к его сожалению, офис компании расположен довольно далеко от дома Кеши. А поскольку в городе проводится спортивный праздник, общественный транспорт ходит крайне редко, и желающих ехать на нём очень много. Впрочем, Кеша уже давно присматривается к электросамокату, и хочет выяснить, много ли усилий ему придётся приложить, чтобы добраться на нём до места работы.
Кеша уже провёл некоторые расчёты и выяснил, что его маршрут содержит в себе ровные участки суммарной длиной p единиц, а также участки, на которых ему придётся подниматься в гору, суммарной длиной m единиц. Участки, на которых Кеша будет двигаться под гору, он решил не учитывать, поскольку электросамокат будет катиться на таких участках по инерции.
При движении по ровному участку аккумулятор самоката будет расходовать 1 единицу ёмкости, а при движении в гору — 2 единицы ёмкости на единицу длины. Если же Кеша не будет включать электродвигатель, то для перемещения на каждой единице длины ровного участка ему потребуется приложить усилие величины a, а на каждой единице длины участка, ведущего в гору, ему потребуется приложить усилие величины b (b > a).
Ёмкость аккумулятора составляет q единиц. Кеша полагает, что в разные дни он может включать электродвигатель на разных участках. И пока хочет узнать, какое максимальное и какое минимальное количество усилий ему придётся приложить, чтобы добраться до работы, если по дороге он полностью израсходует энергию, запасённую в аккумуляторе.
В первой строке содержатся целые числа p, m, a, b, q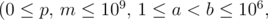 
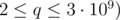, где p — суммарная длина ровных участков, m — суммарная длина участков, на которых нужно двигаться в гору, a — усилие, необходимое для перемещения на единицу длины при движении по ровному участку, b — усилие, необходимое для перемещения на единицу длины при движении в гору, q — ёмкость аккумулятора.
Гарантируется, что числа p и m не равны нулю одновременно; также гарантируется, что числа p и q — чётные.
Выведите два целых числа — минимальное и максимальное количество усилий, которое Кеша может потратить на дорогу, если при этом он полностью израсходует аккумулятор.
Разделяйте числа пробелом или переводом строки.
Подзадача 1 (до 10 баллов)
0 ≤ p, m ≤ 103, 1 ≤ a < b ≤ 103, 2 ≤ q ≤ 3·103, при этом либо p = 0, либо m = 0.
Баллы начисляются за каждый пройденный тест, по запросу сообщаются результаты проверки на каждом тесте.
Подзадача 2 (до 10 баллов)
0 ≤ p, m ≤ 102, 1 ≤ a < b ≤ 102, 2 ≤ q ≤ 3·102
Баллы начисляются за каждый пройденный тест, по запросу сообщаются результаты проверки на каждом тесте.
Подзадача 3 (80 баллов)
Входные данные могут принимать любые допустимые значения.
Баллы начисляются в случае прохождения всех тестов группы.
По запросу сообщается номер первого непройденного теста в группе.
0 5 2 8 4
24
24
4 0 4 16 12
0
0
8 12 5 11 20
62
66
8 10 5 10 20
40
40
6 6 5 7 20
0
0
Поясним приведённые примеры.
В первом примере ровных участков нет вовсе, а в гору Кеше придётся подниматься на участках суммарной длиной 5. К сожалению, ёмкость аккумулятора составляет всего 4 единицы, которых хватит на преодоление участков суммарной длиной 2. Таким образом, усилия, которые Кеше потребуется приложить, равны (5 - 2)·8 = 24. Обратите внимание, что здесь минимальное и максимальное количество необходимых усилий совпадает.
Во втором примере, напротив, отсутствуют участки, на которых нужно ехать в гору. Ёмкость аккумулятора 12, а Кеше нужно проехать всего 4 единицы длины по ровному участку. Так что никаких усилий ему прикладывать не потребуется в принципе.
Обратите внимание, что третий и последующие примеры выходят за рамки ограничений подзадачи 1.
В третьем примере 20 единиц ёмкости аккумулятора можно расходовать по-разному. Например, потратить все 20 единиц на путь в гору (суммарной длиной 10 единиц). Тогда Кеше нужно будет приложить 40 = 8·5 единиц усилий при движении по ровным участкам и 22 = (12 - 10)·11 единицы усилий при движении в гору. Итого это составит 62 единицы усилий. Если же Кеша потратит 8 единиц ёмкости аккумулятора на путь по ровным участкам (суммарной длиной 8 единиц), то оставшейся ёмкости аккумулятора ему хватит на 6 единиц длины пути при движении в гору. А ещё 6 единиц пути в гору потребуют 66 = 11·6 единиц усилий.
В четвёртом примере Кеша может распределить ёмкость аккумулятора разными способами, но во всех случаях ему потребуется 40 единиц усилий на преодоление остающейся части пути.
В пятом примере у Кеши аккумулятор большой ёмкости, которой хватает на весь путь (и ещё немного остаётся), так что никаких усилий ему прикладывать не понадобится.