H. Рождение частицы
Задачу добавил: alef
Успешно сдано решений: 3
Тяжелые частицы, как правило, нестабильны и быстро распадаются. Когда эти тяжелые частицы рождаются в ускорителях, то изучать их приходится по продуктам их распада: траектория тяжелой частицы очень коротка. Нередко процесс распада происходит поэтапно: сначала тяжелая частица распадается на несколько менее тяжелых, а они, в свою очередь, распадаются на множество значительно более легких. Конечно, исследование таких распадов — сложная задача. Вам сейчас предстоит решить значительно более простую. В Вашем распоряжении оказалась «моментальная фотография» одного процесса распада тяжелой частицы. Точка, в которой она распалась, уже известна и обозначена как начало координат.
По предположениям ученых, среди продуктов распада присутствовали в том числе две весьма тяжелые частицы, которые, в свою очередь, породили значительную часть легких частиц, отображенных на «моментальной фотографии». И теперь ученые хотят выделить два пучка, которые (суммарно) содержат наибольшее число частиц.
Назовём радиус-вектором частицы вектор, проведенный из начала координат, к точке, где расположена частица. Назовём частицу с радиус-вектором 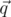 соседней справа для частицы с радиус-вектором
соседней справа для частицы с радиус-вектором 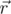 , если при повороте радиус-вектора
, если при повороте радиус-вектора 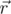 по часовой стрелке на некоторый угол φ его можно совместить с
по часовой стрелке на некоторый угол φ его можно совместить с 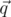 , и при этом не существует никакого другого радиус-вектора, с которым бы
, и при этом не существует никакого другого радиус-вектора, с которым бы 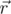 совмещался при повороте по часовой стрелке на угол, меньший φ.
совмещался при повороте по часовой стрелке на угол, меньший φ.
Назовём частицу с радиус-вектором 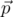 соседней слева для частицы с радиус-вектором
соседней слева для частицы с радиус-вектором 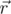 , если при повороте радиус-вектора
, если при повороте радиус-вектора 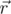 против часовой стрелки на некоторый угол θ его можно совместить с
против часовой стрелки на некоторый угол θ его можно совместить с 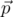 , и при этом не существует никакого другого радиус-вектора, с которым бы
, и при этом не существует никакого другого радиус-вектора, с которым бы 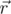 совмещался при повороте против часовой стрелки на угол, меньший θ.
совмещался при повороте против часовой стрелки на угол, меньший θ.
Если одна из частиц является для другой соседней слева или соседней справа, будем говорить, что эти частицы являются соседними.
Назовём пучком с характеристикой α набор из трех или более частиц, для которых выполняются следующие условия:
- Угол между любой парой соседних частиц в этом наборе не превосходит α, а угол между парой соседних частиц, одна из которых входит в этот набор, а другая не входит, превосходит α.
- Радиус-вектор любой частицы набора может быть совмещен с радиус-вектором любой другой частицы набора поворотом, при котором радиус-вектор частицы будет последовательно совмещаться только с радиус-векторами частиц набора.
Некоторая частица может принадлежать либо только одному пучку, либо не принадлежать никакому пучку.
Ваша задача — определить величину α, которая позволит выделить на «моментальной фотографии» два пучка таким образом, чтобы количество частиц в них было максимально возможным. Также следует указать состав каждого из пучков.
Гарантируется, что на «моментальной фотографии» всегда можно выделить хотя бы два пучка частиц.
В первой строке содержится целое число N (6 ≤ N ≤ 105) — количество легких частиц.
В каждой из следующих N строк содержится пара целых чисел через пробел — координаты x и y ( - 10000 ≤ x, y, ≤ 10000) очередной легкой частицы.
В первой строке содержится единственное вещественное число — угол α, позволяющий выделить два пучка, содержащие максимально возможное число частиц.
Во второй строке выведите количество частиц, принадлежащих одному из выделенных пучков. В третьей строке выведите номера частиц, принадлежащих этому пучку, через пробел в порядке возрастания.
В четвертой строке выведите количество частиц, принадлежащих второму из выделенных пучков. В пятой строке выведите номера частиц, принадлежащих этому пучку, через пробел в порядке возрастания.
Вычисления проведите с абсолютной или относительной точностью до 10 - 6.
8
7 0
-5 0
3 5
3 -5
4 5
4 -5
4 4
4 -4
0.134321442
3
3 5 7
3
4 6 8
Пояснение
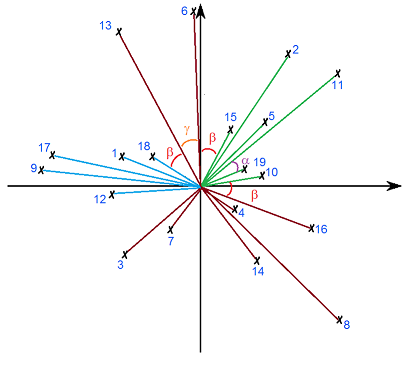
Рисунок не иллюстрирует пример входного файла.
На рисунке показаны два выделенных пучка: из пяти частиц с номерами 1, 9, 12, 17, 18 и из шести частиц с номерами 2, 5, 10, 11, 15, 19. В качестве угла, который позволяет сформировать такие пучки, выбран угол α.
Заметим, что частицы 4, 8, 14, 16 также образуют пучок, но он содержит только четыре частицы.
Если же попытаться выбрать угол β в качестве угла, определяющего пучки, то здесь нас ждет неудача: все частицы, кроме 3 и 7, «сольются» в один пучок (γ < β), а две частицы пучком не являются.
