Плитка (100 баллов)
Задачу добавил: alef
Успешно сдано решений: 7
Для ремонта ванной комнаты была приобретена очень модная N-угольная плитка. Но, поскольку укладывать ее придется на прямоугольные стены, некоторые плитки нужно будет разрезать. Для того чтобы отрезанный кусочек можно было использовать (чтобы он не крошился и не ломался), у него должна быть только одна «внутренняя» (т.е. образованная в результате разреза) сторона. Возникает интересный вопрос: сколькими способами можно отрезать от плитки K кусочков, пригодных для использования? Для определенности будем рассматривать только те случаи, когда разрезы проводятся от вершины к вершине, и в результате остается не более одного «непригодного» кусочка, причем все стороны этого кусочка (если он остается) – внутренние. Кроме того (чтобы не учитывать варианты, образующиеся при поворотах плитки), будем полагать, что один из разрезов всегда должен проходить через некоторую фиксированную вершину (см. рис).
Ваша задача – написать программу, которая подсчитает количество способов для заданных N и K при указанных ограничениях
Формат входного файла input.txt
Первая строка – два целых числа N и K через пробел (3<N<=45, 1<=K<=N)
Формат выходного файла output.txt
Первая строка – целое число – количество способов отрезания K кусочков от плитки
Примечание. Гарантируется, что ответ не превышает 2^31
Пример входного файла
8 3
Пример выходного файла
6
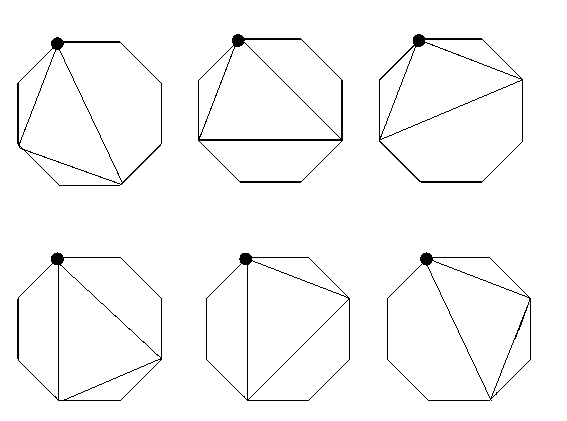
Пояснение к выходному файлу
На рисунке приведены все способы отрезания от 8-угольной плитки 3 кусочков с соблюдением условия задачи. Жирной точкой отмечена фиксированная вершина